Discretisation -- Equal Widths

 

Discretisation or Binning, the process of dividing the data into equal intervals or bins. Yes, we have studied this explanation but how we can do it? 

Still, this question keeps running into our minds... Sit back and relax we have got you covered... 

Here we are going to learn simple and easy techniques that we use in our daily life also -- dividing the data into equal intervals. i.e we divide the into N-equal groups of the same width(gaps). 

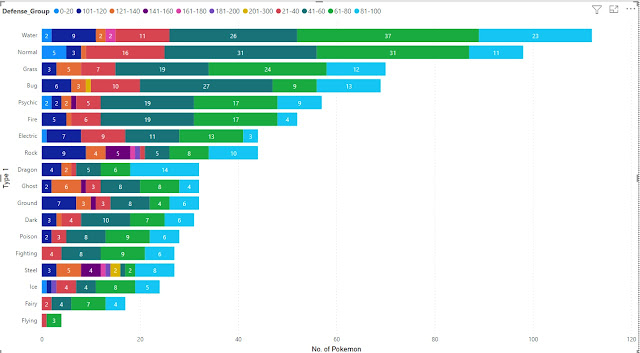Equal Width Binning Example

  

Let's understand it better using the above example(image). Here we had values ranging from 0-300, quite a large width or range for doing any analysis and visualisation. Thus, we decided to divide the data into equal widths of 20(bins of 20), i.e 0-20,21-40,41-60* and so on.

* We used 21,41,61,... because we wanted to make clear that range is inclusive of the upper limit.

Doing so we were able to group the data into 15 bins which not only made it easy to visualize but also helps in analysing the data better and easily.

How to decide Bin Widths? 

So by now, we know that we have to divide the data into some bins of equal widths, but how do we decide what should be the perfect size for our bins. 

Don't worry, we can solve this issue just with a simple formula. Here We Go:- 

Size of Bins = (Maximum Value - Minimum Value) / (Number of Bins)

Here, the number of bins can be decided by the user, that is suppose our data is very widely spread we can select less number of bins to accommodate more data per bin if data is not much spread we can select a high bin count for a good distribution of data.

Eg:- Let's understand it better from our above example.

Maximum Value = 300 

Minimum value = 0 

Number of bins we want = 15 

Using above formula,   (300 - 0) / 15  = 20.

Thus, we had bins of size 20. (0-20,21-40 and so on).

Practical 

We will be using the feature-engine library of python for demo purposes.

1. Importing the Libraries

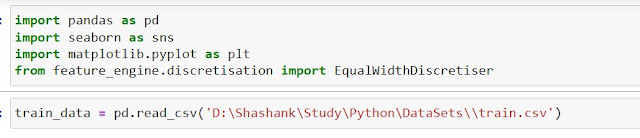Importing Equal Width Discretiser, libraries and data

2. Data Visualization

Since, we will be using only "Age" column of the data set for Discretisation, let's see how it looks when we visualise it. 

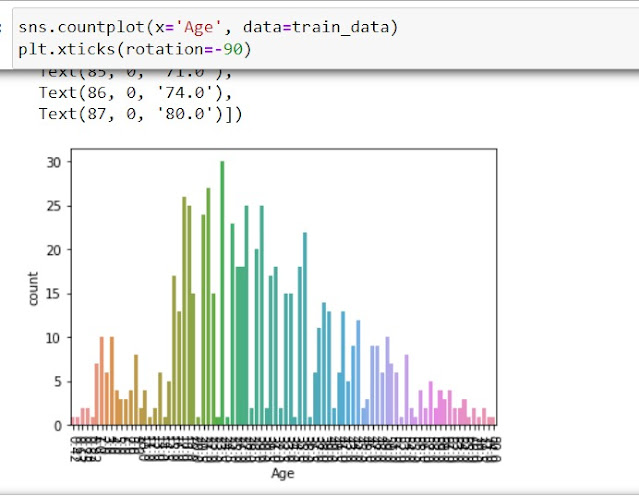Data Visuals before Binning

We can see here that the labels on X-axis are very close and way too many to be read and easily understood. Also, there are too many bars closely packed in the graph, which makes it more difficult to analyse. 

3. Using the Equal Width Discretiser

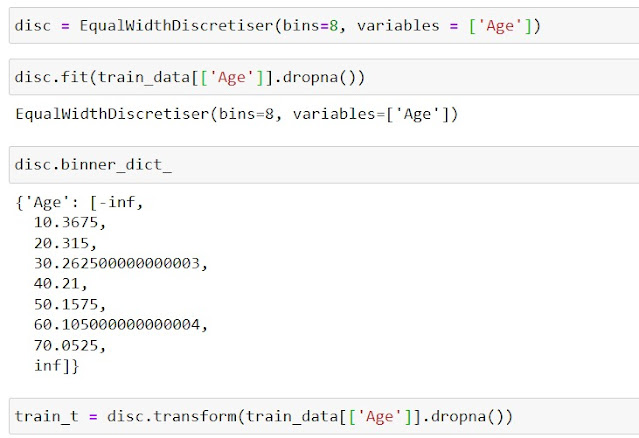Initializing the Equal Width Discretiser

In first line we have initialized the Equal Width Discretiser, then used to fit it on "Age" column.

Once we are done with it, using the "binner_dict_" function we can see that the function has created bins automatically. 

4. Visualizing the End Result

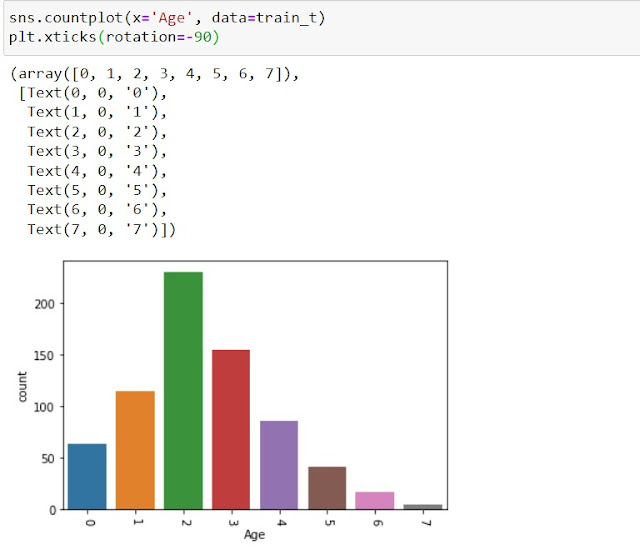Equal Width Discretisation Result

We could notice here that the shape of the original graph is retained in the final result, i.e. higher values in middle, least on the right end. Only we have reduced the number of data presented on the X-axis of graph.

 

Resources

Please comment below to get the complete dataset and libraries. 

Learn to install Anaconda Here.

Learn about the Feature-Engine library Here.

Summary 

In this Quick Reads, we studied a technique, Equal Width Discretisation that is commonly used for Discretisation. We had a quick overview of the technique, understood how and why to use it and some quick Points to Remember. 

We also performed a practical demo of this technique using a famous python library "feature-engine". 

 Last but not least... "Practice Makes One Perfect". So what are you waiting for practice this technique and comment below your views, doubts or anything? We are here to help you.